Pīkau 19: Error detection and correction

Introduction

Why this matters

If you had no way of knowing whether a file that we open might have a few characters changed by a faulty disk, would you use it? If a fault in a network connection causes just one character to change in a document or web page, or one wrong number in a spreadsheet, it could create havoc. We want to know the information that our digital systems download and store is saved correctly, or at least it should warn us if the data has been corrupted.

Detecting and correcting errors occurs all the time on digital devices, and appears in the CT progress outcomes:

PO4: Students understand that digital devices represent data with binary digits and have ways of detecting errors in data storage and transmission.
PO7: Students analyse concepts in digital technologies (for example, ..., error control, ...) by explaining the relevant mechanisms that underpin them.

Links to existing knowledge

You might already know some of this.

When you have to share information that is very important to get exactly right (perhaps reading out a credit card number to someone, or completing a passport application), you probably take measures to make sure they record it correctly. Perhaps you asked them to read it back to you, or you read it twice. For parts that might be hard to understand (like saying the letter “M”) you might add extra information like saying “M for mahi”.

In situations where these details are crucial, you may have heard a phonetic alphabet being used, such as “November Zulu” instead of NZ to spell out details. It is also used by the military; for example, checkpoints A, B and C would be referred to as checkpoints alfa, bravo and charlie.

On digital systems data can also be vulnerable to being received incorrectly, for example, by interference from outside electrical signals or dust landing on the surface of a DVD. Luckily there are efficient and reliable ways to make sure that we can be sure the data we’re working with is the same as what was stored or transmitted. You will have experienced this using digital devices, but since it prevents errors from happening, you probably didn’t notice it! One place that it is explicitly visible is when you scan the barcode on a product in a supermarket. This system can detect if there’s an error reading the code, so rather than just charge you for the wrong product, it can alert you that it needs scanning again.

Error correction as a magic trick

It almost seems like magic that you could receive data, notice that it has been corrupted, and put it back to how it was without asking for another copy. In fact, here’s how the concept can be introduced to students as a magic trick.

This method of error correction is called “Parity error correction”. The word “parity” simply means keeping things equal, and is often used to refer to whether a number is odd or even (since an even number can be split into two equal parts).

The trick in the video is explained in more detail in the CS Unplugged “Parity magic” activity.

For fun, here’s a cheesy video relating to this trick.

What is error control?

Find out the logic behind the parity trick, and how far it can go, by watching this video.

Note that “error control” (error detection and correction) is not about debugging. Debugging is about finding errors that you’ve made when you’re writing a computer program, but error control methods are for finding errors caused by outside interference with the data (which is the input and output to a computer program). Error control is particularly important if the data is stored (on disks etc.) or transmitted (over networks), because the mechanisms we use rely on very dense storage (billions of bits on a small surface area) and high speed transmission (millions of bits travelling down a line every second) which are vulnerable to the tiniest glitch, such as dust on a DVD surface, or a small electrical spike near a network.

Extra if interested

This video introduces the idea of error detection in a humorous way.

Activity - what is error control?

The following QR code is the one used in the video.

Try printing it on paper to try the experiment in the video - you could also copy it into a painting program.
Scan it with a QR reader (often the camera function on a mobile phone will recognise a QR code).
Now try changing some of the black and white squares (by drawing on them with a black or white pen, or white-out), to see if it still reads correctly, and at what point the code is unreadable.

Error detection in product codes

Here’s another everyday use of error control. In this case we can detect errors, but we can’t correct them.

There are a few ways that error detection in a product code can be presented for classroom use. In the video we used the approach of checking that the sum is a multiple of 10, but it can also be presented as a kind of mind-reading trick, where students give you all the digits except the last one, and you work out what the last digit (the check digit) should be so that the total adds up to a multiple of 10. Also, because every second digit is multiplied by 3, it can be easier to write them in alternating rows, add the row and multiple the total by 3, which gives the same result.

There’s more detail on this approach at CS Unplugged: Product code check digits.

Check digits can also be found at the end of other large numbers where a small error could cause a big problem, for example:

credit card numbers
bank account numbers
tax numbers
ISBN (10-digit and 13-digit).

You can find more information about check digits in the CS Field Guide, which has enough detail to address the requirements of CT Progress Outcome 7 - CS Field Guide: Check digits on barcodes.

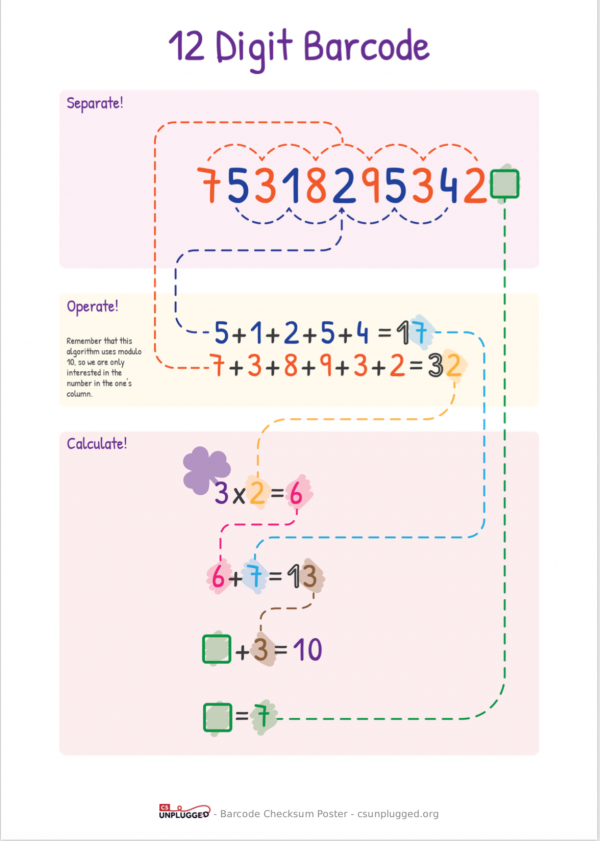
Barcode Checksum Poster

The following Barcode Checksum Poster shows a quick way to calculate the checksum in a product code. It is for 13-digit product codes, which are the most common in New Zealand.

12-digit product codes are common in the US, and 8-digit codes are sometimes used for small products, but it should be easy to find plenty of items with 13-digit product codes in the stationery cupboard or recycling bin.

CS Unplugged: Barcode Checksum Poster

Reflect and connect

Organisations often assign you a number, such as a tax number, credit card number, loyalty card number, and so on. How many numbers do you have that identify you to an organisation? If you have a wallet full of cards, that might provide a few reminders!
When you use these numbers with an organisation it’s crucial that they are accurate, whether you’re reading out the number or swiping the card. In nearly every case you’ll find that they contain a check digit to avoid awkward or confusing situations, such as having your passport number scanned as someone else’s.
This raises some interesting ethical questions. Why can’t we just identify people by their name? And why don’t all systems that need a number just use the same number for an individual, to save having lots of numbers to keep track of?

Link to programme design

Technological practice

Practically all digital data has error control added to it to make systems more reliable. In general situations (such as storing on disk or downloading on the internet) the error control is built into the subsystems and is only noticeable because the capacity of devices seems to be less than it should be (due to extra error control bits taking up some of the space). In other situations it needs to be added explicitly, and designers need to make a tradeoff between the amount of space (bits or digits) allocated to error control, and the reliability of the system.

To connect this practice to the NZC in your programme, refer to Outcome Development and Evaluation.

Technological knowledge

When designing a digital system, incorporating error control is a powerful tool to test the validity of data, enable data to be transmitted in “noisy” environments (for example, across a farm with electric fences), and even verify that data hasn’t been interfered with deliberately. This knowledge opens up many new possibilities. To incorporate this knowledge refer to Technological Systems.

Nature of technology

The capability of digital technology to store things very accurately is both a positive (valuable information can be accessed reliably) and a negative (once something is in digital form, it’s very hard to get rid of it). Without error control techniques this wouldn’t be the case; valuable information might get corrupted, and incriminating information could be passed off as a computer error. Once they understand error control, students can explore the longevity of information, both the benefits and problems, in a new way. Refer to Characteristics of Technological Outcomes for more information.

Error control systems based on a check digit (such as product codes and ISBN numbers) are easily calculated by hand, and provide an opportunity to exercise basic maths facts, where getting the check digit right indicates that they have done their calculations correctly.

An ISBN-10 number (used on books prior to 2007) multiplies by all 10 digits, so is particularly good for this. If an exercise is run in the library (or looking at book covers online), it also gives students a chance to identify which books published prior to 2007 are still accessible.

The prefixes on product codes also provide an interesting insight into politics and commerce.

For example, a prefix of 94 indicates that the barcode was registered in New Zealand, whereas 93 is from Australia.
But have disputed territories, such as Tibet and Palestine, been allocated prefixes?
Is Hong Kong separate from China?
And who allocates codes to countries, and how are they allocated within each country?

Wrapping up and where to next?

The examples here have focused on error control where it is most visible (literally), especially for QR codes and product codes. The less visible error control systems protect the billions of bits that are stored on and transmitted between computers, and use much more sophisticated mathematical methods.

When dealing with large amounts of data:

error control is one of three ways that data is “coded”
the other two are compression (to make files smaller and transmission faster)
and encryption (to make files almost impossible to access even if they are intercepted by an eavesdropper).

Often all three forms of “coding” are applied to data; for example, if you take a photo on a camera then it is typically compressed to a smaller size using the JPEG method, transmitted through wireless using encryption, and has error correction codes applied to make sure that all the data gets through correctly.

Techniques for compression and encryption are explored at NCEA level, and they build on the ideas around binary representation that appear up to CT Progress Outcome 5.